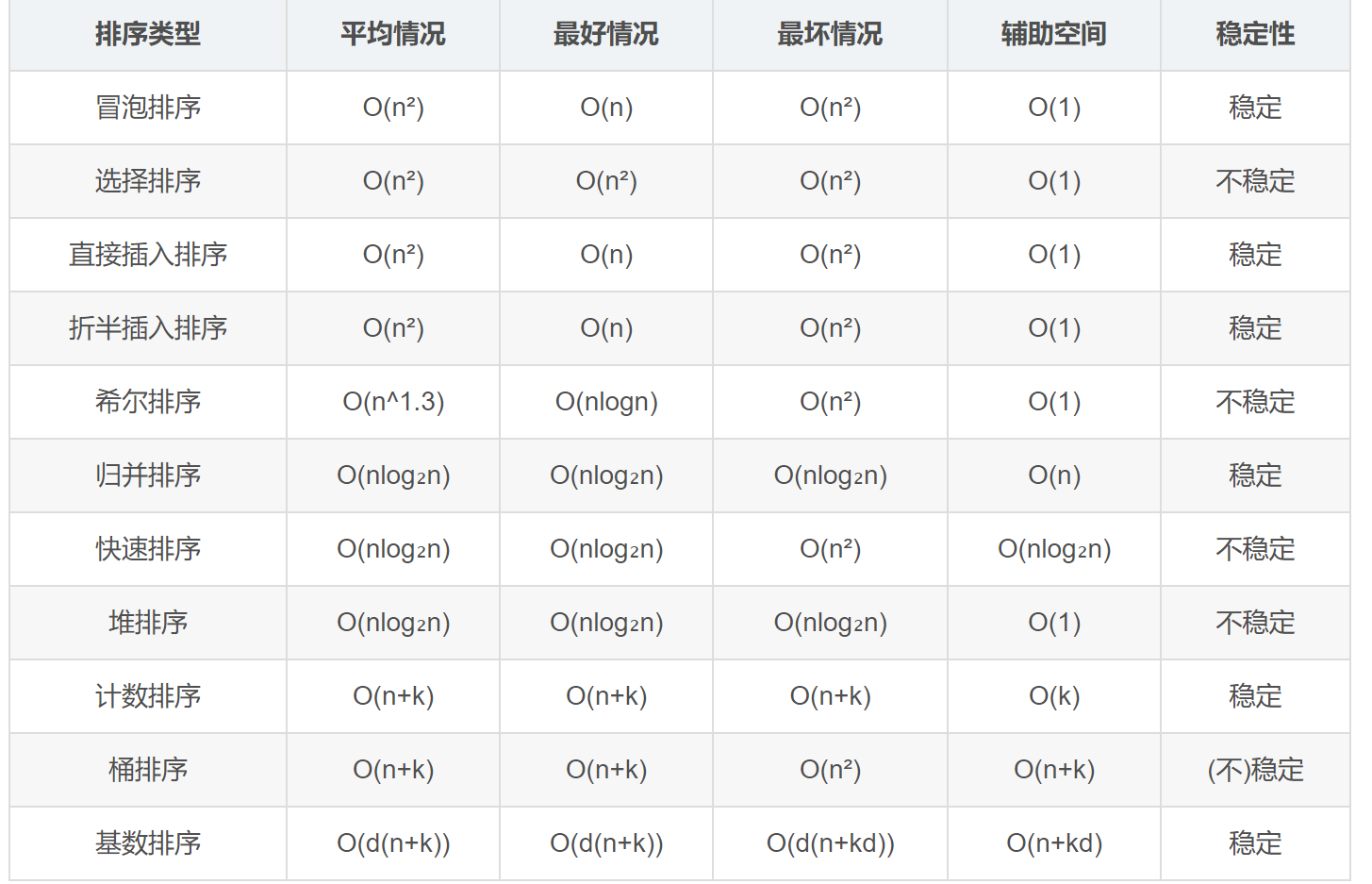
排序算法
冒泡排序
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。
- 这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。

public static void bubbleSort(int arr[]) {
for(int i =0 ; i<arr.length-1 ; i++) {
for(int j=0 ; j<arr.length-1-i ; j++) {
if(arr[j]>arr[j+1]) {
int temp = arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
}
}选择排序
- 首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置
- 再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
- 重复第二步,直到所有元素均排序完毕。

public static void selectionSort(int[] arr){ for(int i = 0; i < arr.length - 1; i++){ // 交换次数 // 先假设每次循环时,最小数的索引为i int minIndex = i;// 每一个元素都和剩下的未排序的元素比较 for(int j = i + 1; j < arr.length; j++){ if(arr[j] < arr[minIndex]){//寻找最小数 minIndex = j;//将最小数的索引保存 } }//经过一轮循环,就可以找出第一个最小值的索引,然后把最小值放到i的位置 swap(arr, i, minIndex); } } private static void swap(int[] arr, int i, int j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; }
插入排序
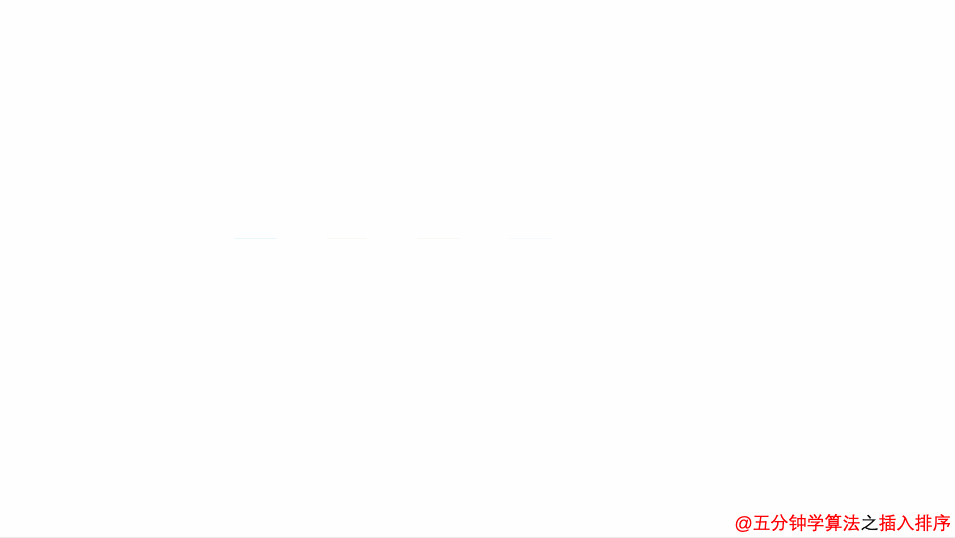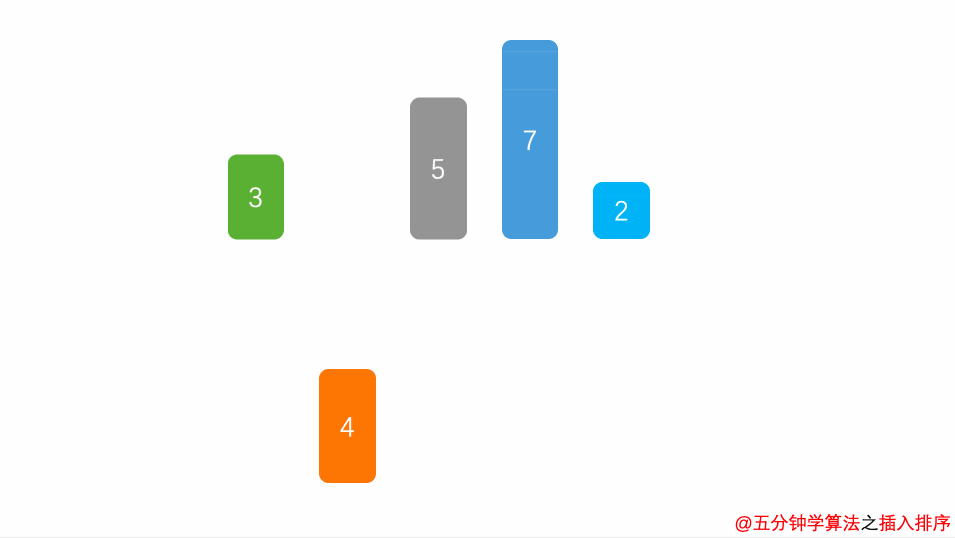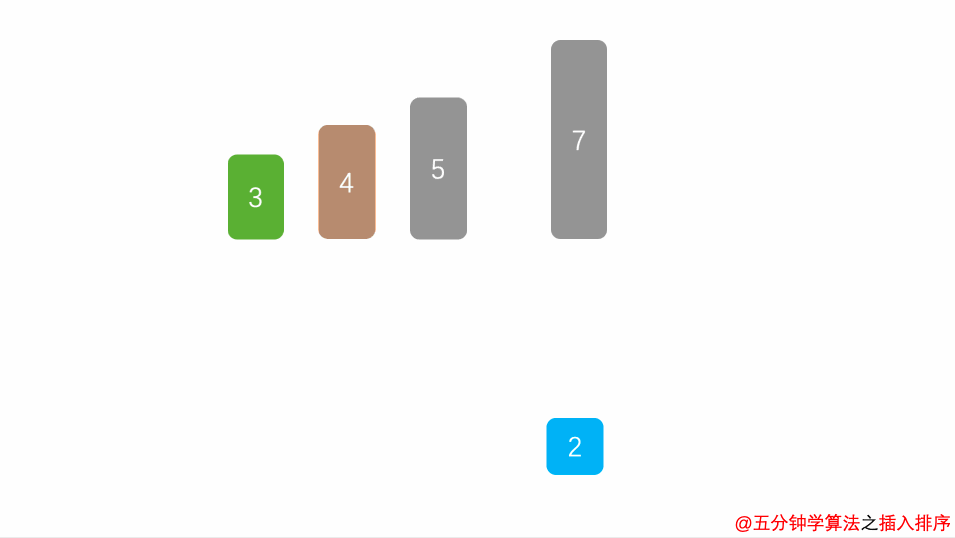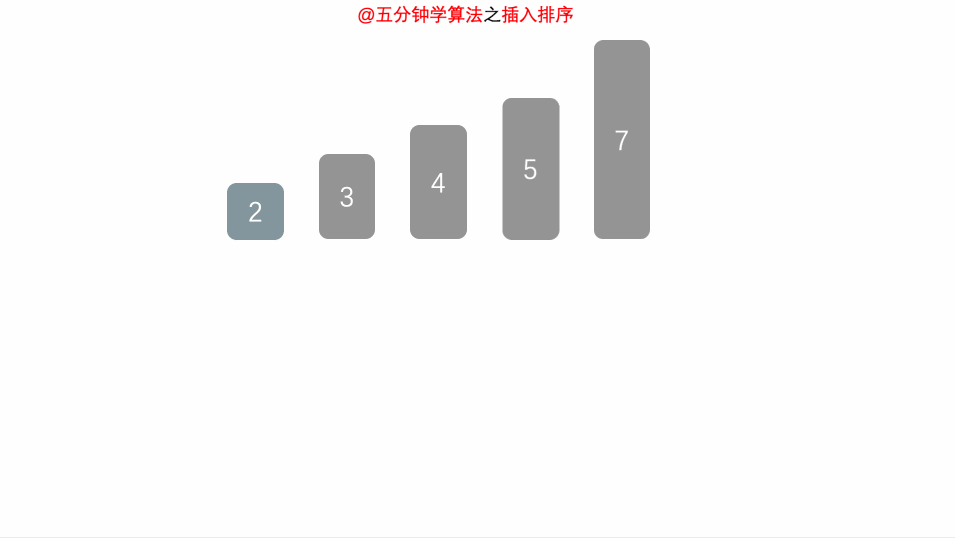
- 将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
- 从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。
- (如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。)
public class Insertion
{
public static void sort(Comparable[] a)
{
//将a[]按升序排列
int N=a.length;
for (int i=1;i<N;i++)
{
//将a[i]插入到a[i-1],a[i-2],a[i-3]……之中
for(int j=i;j>0&&(a[j].compareTo(a[j-1])<0);j--)
{
Comparable temp=a[j];
a[j]=a[j-1];
a[j-1]=temp;
}
}
}
}希尔排序
- 选择一个增量序列 t1,t2,……,tk,其中 ti > tj, tk = 1;
- 按增量序列个数 k,对序列进行 k 趟排序;每趟排序,根据对应的增量 ti,将待排序列分割成若干长度为 m 的子序列,分别对各子表进行直接插入排序。
- 仅增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。

public static void main(String[] args){ int[] array={49,38,65,97,76,13,27,49,78,34,12,64,1}; System.out.println("排序之前:"); for(int i=0;i<array.length;i++){ System.out.print(array[i]+" "); } //希尔排序 int gap = array.length; while (true) { gap /= 2; //增量每次减半 for (int i = 0; i < gap; i++) { for (int j = i + gap; j < array.length; j += gap) {//这个循环里其实就是一个插入排序 int k = j - gap; while (k >= 0 && array[k] > array[k+gap]) { int temp = array[k]; array[k] = array[k+gap]; array[k + gap] = temp; k -= gap; } } } if (gap == 1) break; } System.out.println(); System.out.println("排序之后:"); for(int i=0;i<array.length;i++){ System.out.print(array[i]+" "); } }
归并排序
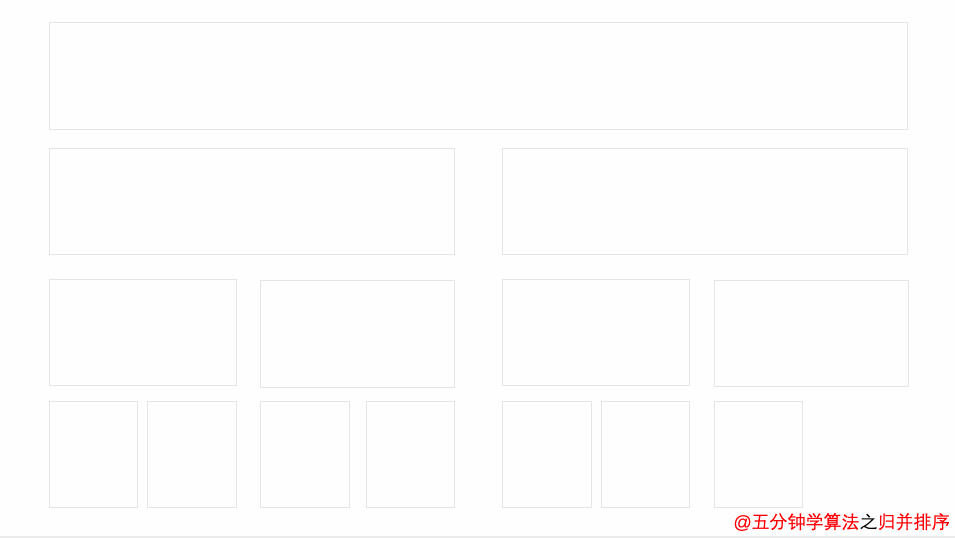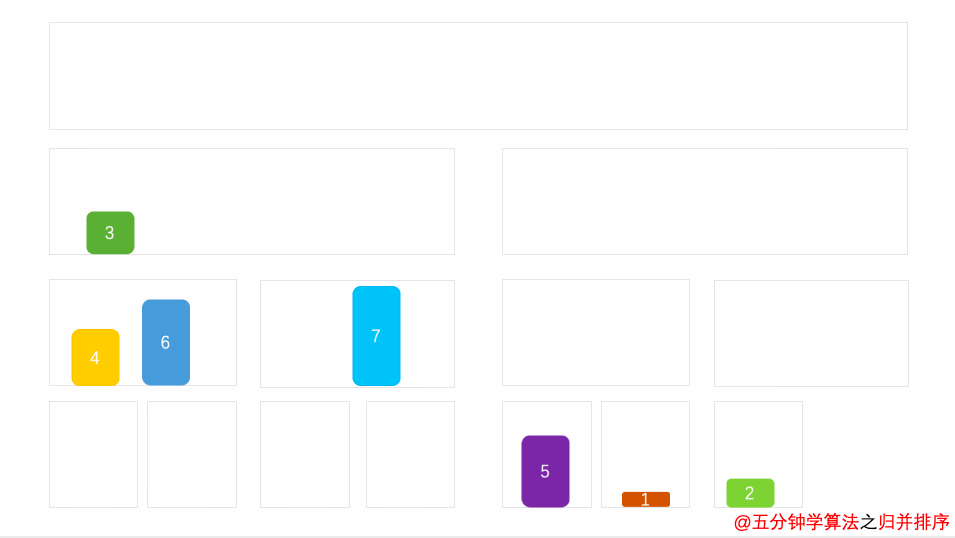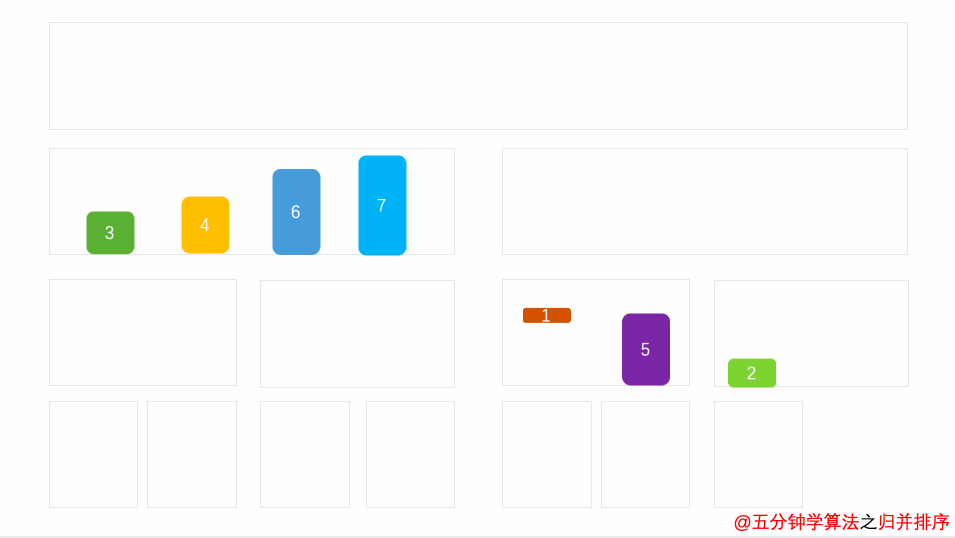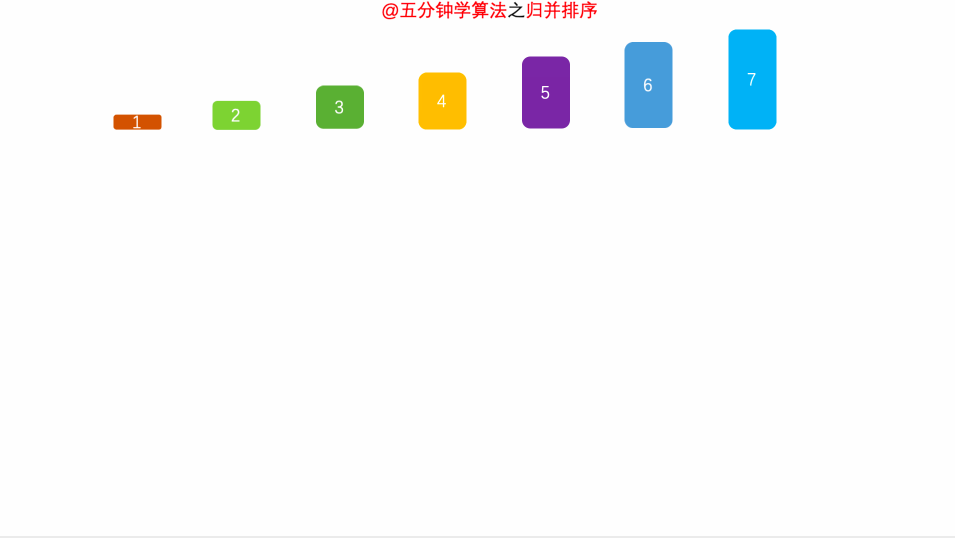
- 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置;
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
- 重复步骤 3 直到某一指针达到序列尾;将另一序列剩下的所有元素直接复制到合并序列尾。
package MergeSort; public class MergeSort { public static int[] mergeSort(int[] nums, int l, int h) { if (l == h) return new int[] { nums[l] }; int mid = l + (h - l) / 2; int[] leftArr = mergeSort(nums, l, mid); //左有序数组 int[] rightArr = mergeSort(nums, mid + 1, h); //右有序数组 int[] newNum = new int[leftArr.length + rightArr.length]; //新有序数组 int m = 0, i = 0, j = 0; while (i < leftArr.length && j < rightArr.length) { newNum[m++] = leftArr[i] < rightArr[j] ? leftArr[i++] : rightArr[j++]; } while (i < leftArr.length) newNum[m++] = leftArr[i++]; while (j < rightArr.length) newNum[m++] = rightArr[j++]; return newNum; } public static void main(String[] args) { int[] nums = new int[] { 9, 8, 7, 6, 5, 4, 3, 2, 10 }; int[] newNums = mergeSort(nums, 0, nums.length - 1); for (int x : newNums) { System.out.println(x); } } }快速排序
- 从数列中挑出一个元素,称为 “基准”(pivot);
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。
- 在这个分区退出之后,该基准就处于数列的中间位置。
- 这个称为分区(partition)操作;
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序;

堆排序
- 创建一个堆 H[0……n-1];
- 把堆首(最大值)和堆尾互换;
- 把堆的尺寸缩小 1,并调用 shift_down(0),目的是把新的数组顶端数据调整到相应位置;
- 重复步骤 2,直到堆的尺寸为 1。

public class HelloWorld {
/**
* 选择排序-堆排序
* @param array 待排序数组
* @return 已排序数组
*/
public static int[] heapSort(int[] array) {
//这里元素的索引是从0开始的,所以最后一个非叶子结点array.length/2 - 1
for (int i = array.length / 2 - 1; i >= 0; i--) {
adjustHeap(array, i, array.length); //调整堆
}
// 上述逻辑,建堆结束
// 下面,开始排序逻辑
for (int j = array.length - 1; j > 0; j--) {
// 元素交换,作用是去掉大顶堆
// 把大顶堆的根元素,放到数组的最后;换句话说,就是每一次的堆调整之后,都会有一个元素到达自己的最终位置
swap(array, 0, j);
// 元素交换之后,毫无疑问,最后一个元素无需再考虑排序问题了。
// 接下来我们需要排序的,就是已经去掉了部分元素的堆了,这也是为什么此方法放在循环里的原因
// 而这里,实质上是自上而下,自左向右进行调整的
adjustHeap(array, 0, j);
}
return array;
}
/**
* 整个堆排序最关键的地方
* @param array 待组堆
* @param i 起始结点
* @param length 堆的长度
*/
public static void adjustHeap(int[] array, int i, int length) {
// 先把当前元素取出来,因为当前元素可能要一直移动
int temp = array[i];
for (int k = 2 * i + 1; k < length; k = 2 * k + 1) { //2*i+1为左子树i的左子树(因为i是从0开始的),2*k+1为k的左子树
// 让k先指向子节点中最大的节点
if (k + 1 < length && array[k] < array[k + 1]) { //如果有右子树,并且右子树大于左子树
k++;
}
//如果发现结点(左右子结点)大于根结点,则进行值的交换
if (array[k] > temp) {
swap(array, i, k);
// 如果子节点更换了,那么,以子节点为根的子树会受到影响,所以,循环对子节点所在的树继续进行判断
i = k;
} else { //不用交换,直接终止循环
break;
}
}
}
/**
* 交换元素
* @param arr
* @param a 元素的下标
* @param b 元素的下标
*/
public static void swap(int[] arr, int a, int b) {
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
public static void main(String []args) {
int [] A=new int []{1,6,8,9,6,3,4,8,6,3,1,5,2,3,5};
A=heapSort(A)
for(int i=0;i<A.length;i++)
System.out.println(A[i]);
}
}计数排序
- 花O(n)的时间扫描一下整个序列 A,获取最小值 min 和最大值
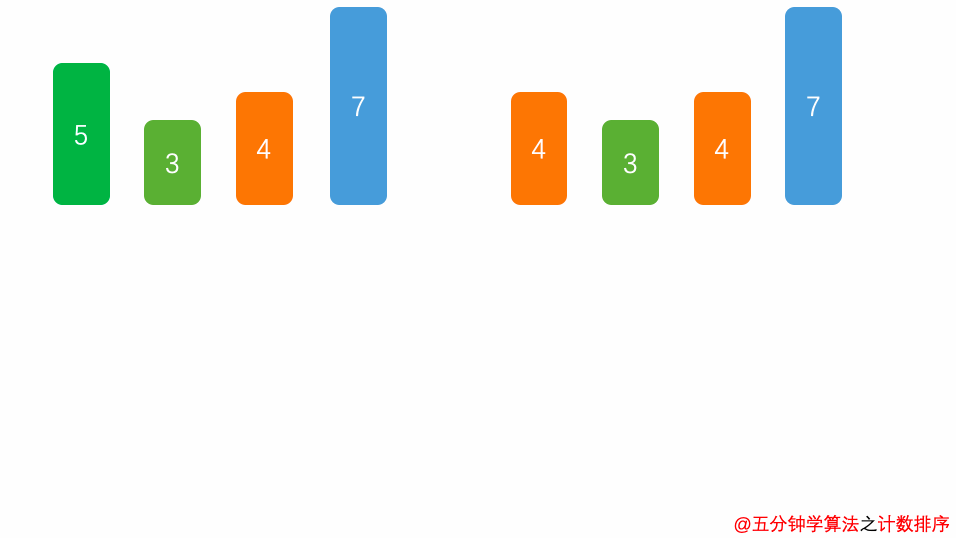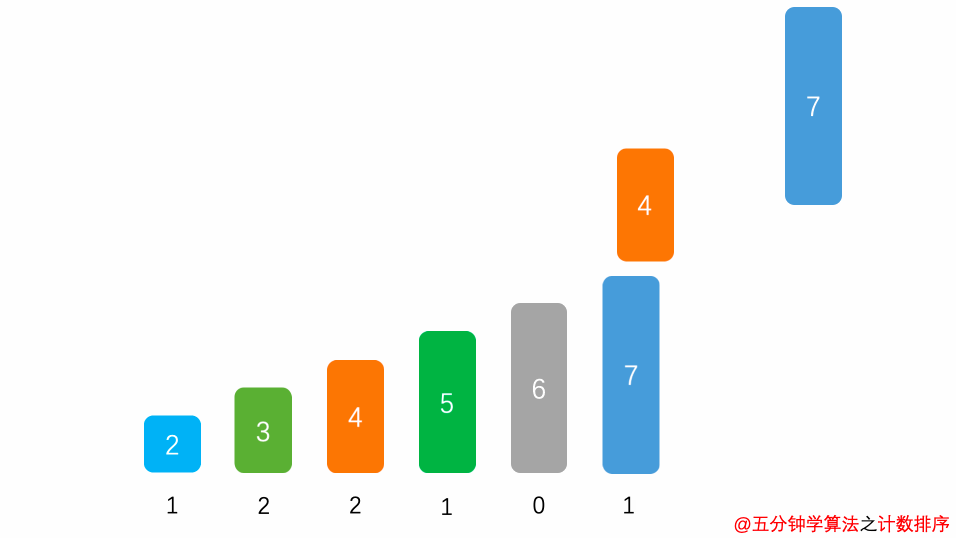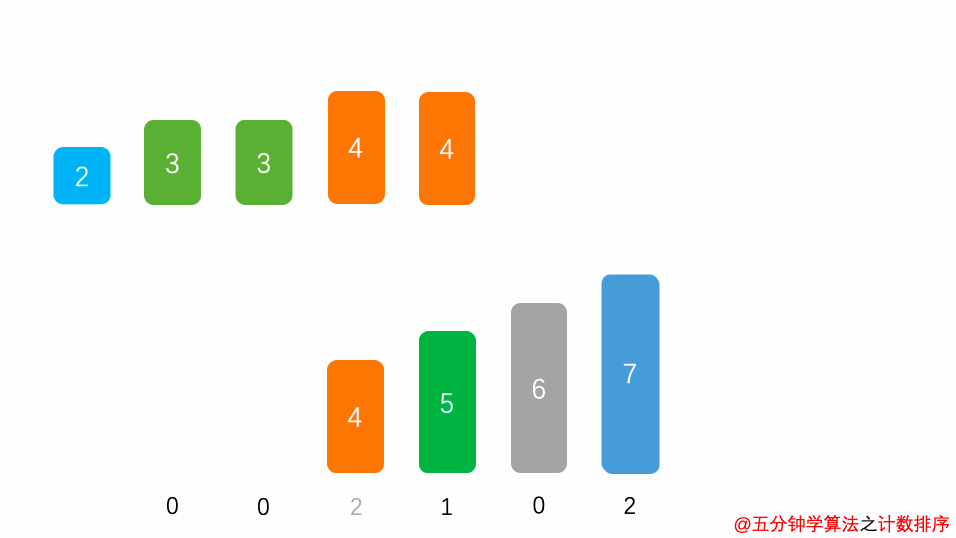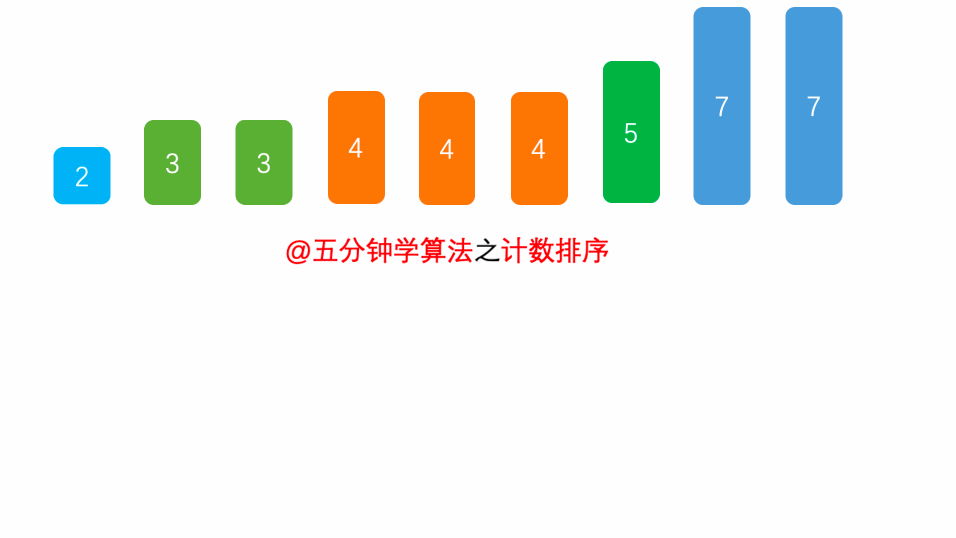
- max开辟一块新的空间创建新的数组 B,长度为 ( max - min + 1)
- 数组 B 中 index 的元素记录的值是 A 中某元素出现的次数
最后输出目标整数序列,具体的逻辑是遍历数组 B,输出相应元素以及对应的个数
//针对c数组的大小,优化过的计数排序 publicclassCountSort{ publicstaticvoidmain(String[]args){ //排序的数组 int a[]={100,93,97,92,96,99,92,89,93,97,90,94,92,95}; int b[]=countSort(a); for(inti:b){ System.out.print(i+""); } System.out.println(); } public static int[] countSort(int[]a){ int b[] = new int[a.length]; int max = a[0],min = a[0]; for(int i:a){ if(i>max){ max=i; } if(i<min){ min=i; } }//这里k的大小是要排序的数组中,元素大小的极值差+1 int k=max-min+1; int c[]=new int[k]; for(int i=0;i<a.length;++i){ c[a[i]-min]+=1;//优化过的地方,减小了数组c的大小 } for(int i=1;i<c.length;++i){ c[i]=c[i]+c[i-1]; } for(int i=a.length-1;i>=0;--i){ b[--c[a[i]-min]]=a[i];//按存取的方式取出c的元素 } return b; } }桶排序
设置固定数量的空桶。
- 把数据放到对应的桶中。
- 对每个不为空的桶中数据进行排序。
- 拼接不为空的桶中数据,得到结果

public static void basket(int data[])//data为待排序数组 { int n=data.length; int bask[][]=new int[10][n]; int index[]=new int[10]; int max=Integer.MIN_VALUE; for(int i=0;i<n;i++) { max=max>(Integer.toString(data[i]).length())?max:(Integer.toString(data[i]).length()); } String str; for(int i=max-1;i>=0;i--) { for(int j=0;j<n;j++) { str=""; if(Integer.toString(data[j]).length()<max) { for(int k=0;k<max-Integer.toString(data[j]).length();k++) str+="0"; } str+=Integer.toString(data[j]); bask[str.charAt(i)-'0'][index[str.charAt(i)-'0']++]=data[j]; } int pos=0; for(int j=0;j<10;j++) { for(int k=0;k<index[j];k++) { data[pos++]=bask[j][k]; } } for(intx=0;x<10;x++)index[x]=0; } }基数排序
- 将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零
- 从最低位开始,依次进行一次排序
- 从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列

public class RadixSort
{
public static void sort(int[] number, int d) //d表示最大的数有多少位
{
intk = 0;
intn = 1;
intm = 1; //控制键值排序依据在哪一位
int[][]temp = newint[10][number.length]; //数组的第一维表示可能的余数0-9
int[]order = newint[10]; //数组order[i]用来表示该位是i的数的个数
while(m <= d)
{
for(inti = 0; i < number.length; i++)
{
intlsd = ((number[i] / n) % 10);
temp[lsd][order[lsd]] = number[i];
order[lsd]++;
}
for(inti = 0; i < 10; i++)
{
if(order[i] != 0)
for(intj = 0; j < order[i]; j++)
{
number[k] = temp[i][j];
k++;
}
order[i] = 0;
}
n *= 10;
k = 0;
m++;
}
}
public static void main(String[] args)
{
int[]data =
{73, 22, 93, 43, 55, 14, 28, 65, 39, 81, 33, 100};
RadixSort.sort(data, 3);
for(inti = 0; i < data.length; i++)
{
System.out.print(data[i] + "");
}
}
}排序算法比较