pythonmpu6050

树莓派 python
python
发布日期:   2021-12-20
更新日期:   2021-12-22
文章字数:   2.8k
阅读时长:   15 分
阅读次数:  

树莓派mpu6050_姿态估计

MPU6050是世界上第一款也是唯一一款专为智能手机、平板电脑和可穿戴传感器的低功耗、低成本和高性能要求而设计的6轴运动跟踪设备。

它集成了3轴MEMS陀螺仪，3轴MEMS加速度计，以及一个可扩展的数字运动处理器 DMP（ DigitalMotion Processor），可用I2C接口连接一个第三方的数字传感器，比如磁力计。扩展之后就可以通过其 I2C或SPI接口输出一个9轴的信号（ SPI接口仅在MPU-6000可用）。 MPU-60X0也可以通过其I2C接口连接非惯性的数字传感器，比如压力传感器。

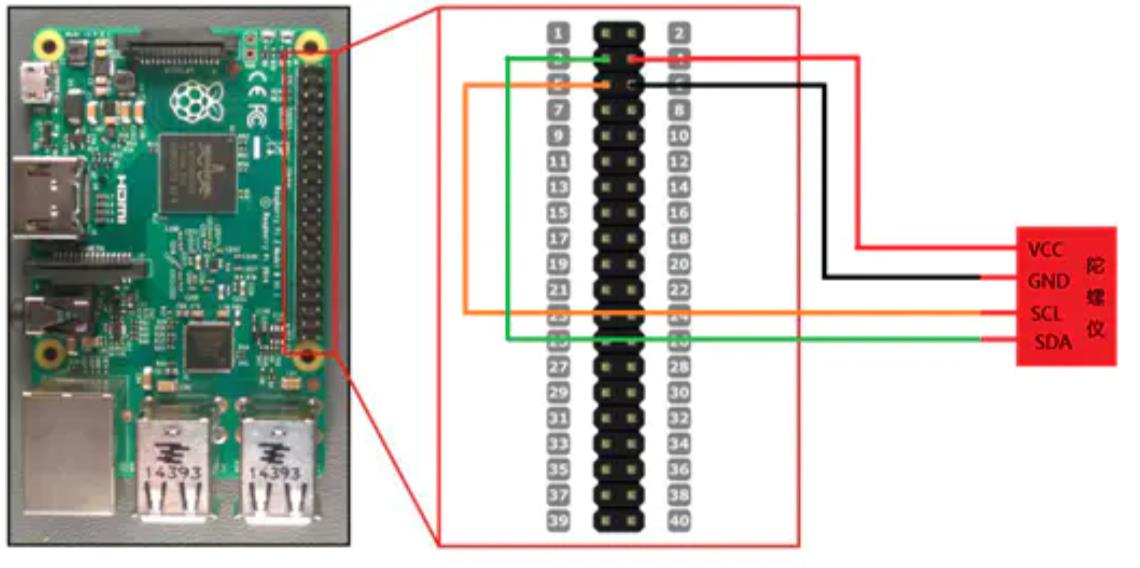
接线及测试

GND —- GND VCC —- 接树莓派 5V

SDA —- I2C 数据 SCL —- I2C 时钟

测试

sudo i2cdetect -y 1
接线没错的话，可以看到MPU6050 地址是 0x68

安装依赖包

pip install mpu6050-raspberrypi
python-smbus或python3-smbus包，根据你的 Python 版本。

使用

  1. 获取温度
    get_temp()
  2. 获取加速度计范围
    def set_accel_range(self, accel_range):
# 设置加速度计范围
 
ACCEL_RANGE_2G = 0x00
ACCEL_RANGE_4G = 0x08
ACCEL_RANGE_8G = 0x10
ACCEL_RANGE_16G = 0x18
  3. 读取加速度计设置的范围
def read_accel_range(self, raw = False):...
 
# 返回: 2, 4, 8, 16
# 返回 -1 时，说明出了问题
  1. 读取加速度计数据
    def get_accel_data(self, g = False):...
    return {'x': x, 'y': y, 'z': z}
  2. 设置陀螺仪范围
    def set_gyro_range(self, gyro_range):...
 
ACCEL_SCALE_MODIFIER_2G = 16384.0
ACCEL_SCALE_MODIFIER_4G = 8192.0
ACCEL_SCALE_MODIFIER_8G = 4096.0
ACCEL_SCALE_MODIFIER_16G = 2048.0
  3. 读取陀螺仪的范围
    def read_gyro_range(self, raw = False):...
 
# 如果raw为真，它将从GIRO配置寄存器返回原始值
# 如果rar为False，它将返回250、500、1000、2000或1。如果返回值等于-1，那么就有问题了。神经网络
  4. 读取陀螺仪数据
    def get_gyro_data(self):...
    return {'x': x, 'y': y, 'z': z}
 
# 获取并返回陀螺仪的X、Y和Z值。
# 返回adictionary中的读取值。
  5. 返回所有数值 
    def get_all_data(self):
    """Reads and returns all the available data."""
    temp = self.get_temp()
    accel = self.get_accel_data()
    gyro = self.get_gyro_data()
 
    return [accel, gyro, temp]

    tuoluoyi.py

    from mpu6050 import mpu6050
sensor = mpu6050(0x68)
accelerometer_data = sensor.get_all_data()

输出

[{'y': 8.86812294921875, 'x': -3.414131567382812, 'z': 1.6017209106445311},
 {'y': 0.8931297709923665, 'x': -1.6870229007633588, 'z': 0.22137404580152673},
  25.941764705882356]

将数据传输到电脑，电脑分析轨迹

树莓派

#coding:utf-8
import datetime
import math
import time

from mpu6050 import mpu6050
from math import cos, sin
import numpy as np
import matplotlib.pyplot as plt
from socket import *
import struct
import numpy
Kp = 100  # 比例增益控制加速度计/磁强计的收敛速度
Ki = 0.002  # 积分增益控制陀螺仪偏差的收敛速度
halft = 0.001  # 采样周期的一半
# 传感器框架相对于辅助框架的四元数（初始化四元数的值）
q0 = 1
q1 = 0
q2 = 0
q3 = 0

# 由Ki缩放的积分误差项（初始化）
exInt = 0
eyInt = 0
ezInt = 0

mpu = mpu6050(0x68)

# [{'y': 8.86812294921875, 'x': -3.414131567382812, 'z': 1.6017209106445311}, {'y': 0.8931297709923665, 'x': -1.6870229007633588, 'z': 0.22137404580152673}, 25.941764705882356]


class Quadrotor():
    def __init__(self, x=0, y=0, z=0, roll=0, pitch=0, yaw=0, size=1, show_animation=True):
        self.p1 = np.array([size / 2, 0, 0, 1]).T
        self.p2 = np.array([-size / 2, 0, 0, 1]).T
        self.p3 = np.array([0, size / 2, 0, 1]).T
        self.p4 = np.array([0, -size / 2, 0, 1]).T

        self.x_data = []
        self.y_data = []
        self.z_data = []
        self.show_animation = show_animation

        if self.show_animation:
            plt.ion()
            fig = plt.figure()
            self.ax = fig.add_subplot(111, projection='3d')

        self.update_pose(x, y, z, roll, pitch, yaw)

    def update_pose(self, x, y, z, roll, pitch, yaw):
        self.x = x
        self.y = y
        self.z = z
        self.roll = roll
        self.pitch = pitch
        self.yaw = yaw
        self.x_data.append(x)
        self.y_data.append(y)
        self.z_data.append(z)

        if self.show_animation:
            self.plot()

    def transformation_matrix(self):
        x = self.x
        y = self.y
        z = self.z
        roll = self.roll
        pitch = self.pitch
        yaw = self.yaw
        return np.array(
            [[cos(yaw) * cos(pitch), -sin(yaw) * cos(roll) + cos(yaw) * sin(pitch) * sin(roll), sin(yaw) * sin(roll) + cos(yaw) * sin(pitch) * cos(roll), x],
             [sin(yaw) * cos(pitch), cos(yaw) * cos(roll) + sin(yaw) * sin(pitch) *
              sin(roll), -cos(yaw) * sin(roll) + sin(yaw) * sin(pitch) * cos(roll), y],
             [-sin(pitch), cos(pitch) * sin(roll), cos(pitch) * cos(yaw), z]
             ])

    def plot(self):
        T = self.transformation_matrix()

        p1_t = np.matmul(T, self.p1)
        p2_t = np.matmul(T, self.p2)
        p3_t = np.matmul(T, self.p3)
        p4_t = np.matmul(T, self.p4)

        plt.cla()

        self.ax.plot([p1_t[0], p2_t[0], p3_t[0], p4_t[0]],
                     [p1_t[1], p2_t[1], p3_t[1], p4_t[1]],
                     [p1_t[2], p2_t[2], p3_t[2], p4_t[2]], 'k.')

        self.ax.plot([p1_t[0], p2_t[0]], [p1_t[1], p2_t[1]],
                     [p1_t[2], p2_t[2]], 'r-')
        self.ax.plot([p3_t[0], p4_t[0]], [p3_t[1], p4_t[1]],
                     [p3_t[2], p4_t[2]], 'r-')

        self.ax.plot(self.x_data, self.y_data, self.z_data, 'b:')

        plt.xlim(-5, 5)
        plt.ylim(-5, 5)
        self.ax.set_zlim(0, 10)

        plt.pause(0.1)
# while True:
def cal_integral(x, y):
    import scipy
    from scipy.integrate import simps  # 用于计算积分

    integrals = []
    for i in range(len(y)):  # 计算梯形的面积，由于是累加，所以是切片"i+1"
        integrals.append(1/2*scipy.integrate.trapz(y[:i + 1], x[:i + 1]))

    return integrals

def cal_tiem(a,s,lt,v=0):
    a=a*gravitational_acceleration
    ct=time.perf_counter()
    v=v+a*(ct-lt)
    s+=a*(ct-lt)**2/2
    lt=ct
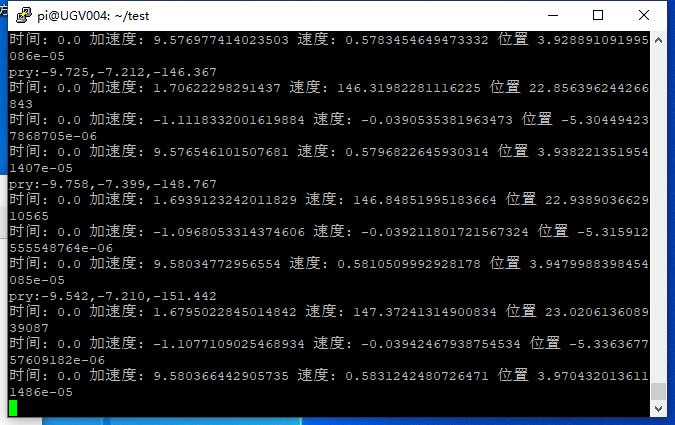
    print("时间:",ct-lt,"加速度:",a,"速度:",v,"位置",s)
    return lt,s,v


def KalmanFilter(z, n_iter=20):
    # 这里是假设A=1，H=1的情况

    # intial parameters

    sz = (n_iter,)  # size of array

    # Q = 1e-5 # process variance
    Q = 1e-6  # process variance
    # allocate space for arrays
    xhat = numpy.zeros(sz)  # a posteri estimate of x
    P = numpy.zeros(sz)  # a posteri error estimate
    xhatminus = numpy.zeros(sz)  # a priori estimate of x
    Pminus = numpy.zeros(sz)  # a priori error estimate
    K = numpy.zeros(sz)  # gain or blending factor

    R = 0.1 ** 2  # estimate of measurement variance, change to see effect

    # intial guesses
    xhat[0] = 0.0
    P[0] = 1.0
    A = 1
    H = 1

    for k in range(1, n_iter):
        # time update
        xhatminus[k] = A * xhat[k - 1]  # X(k|k-1) = AX(k-1|k-1) + BU(k) + W(k),A=1,BU(k) = 0
        Pminus[k] = A * P[k - 1] + Q  # P(k|k-1) = AP(k-1|k-1)A' + Q(k) ,A=1

        # measurement update
        K[k] = Pminus[k] / (Pminus[k] + R)  # Kg(k)=P(k|k-1)H'/[HP(k|k-1)H' + R],H=1
        xhat[k] = xhatminus[k] + K[k] * (z[k] - H * xhatminus[k])  # X(k|k) = X(k|k-1) + Kg(k)[Z(k) - HX(k|k-1)], H=1
        P[k] = (1 - K[k] * H) * Pminus[k]  # P(k|k) = (1 - Kg(k)H)P(k|k-1), H=1
    return xhat

HOST ='192.168.3.108'
PORT = 12345
BUFFSIZE=2048
ADDR = (HOST,PORT)
tctimeClient = socket(AF_INET,SOCK_STREAM)
tctimeClient.connect(ADDR) #发送 tctimeClient.send("发送内容".encode) reciverdata=tctimeClient.recv(bufsize).decode()


position=[0,0,0]
Vv=[0,0,0]
gravitational_acceleration=9.793#武汉
lt = time.perf_counter()

while True:
    aaxx=[]
    aayy=[]
    aazz=[]
    for i in range(50):
        accel = mpu.get_accel_data() # 加速度
        gyro = mpu.get_gyro_data() # 角速度
        aax = accel['x']  # 原始加速度x轴数据
        aay = accel['y']  # 原始加速度y轴数据
        aaz = accel['z']  # 原始加速度z轴数据
        print("x轴加速度",aax)
        aaxx.append(aax)
        aayy.append(aay)
        aazz.append(aaz-1)

        ggx = gyro['x']  # 原始角速度x轴数据
        ggy = gyro['y']   # 原始角速度y轴数据
        ggz = gyro['z']  # 原始角速度z轴数据

        # 把csv的字符串转化为float型
        ax = float(aax)
        ay = float(aay)
        az = float(aaz)
        gx = float(ggx)
        gy = float(ggy)
        gz = float(ggz)

        # 单元化
        norm = math.sqrt(ax * ax + ay * ay + az * az)
        ax = ax / norm
        ay = ay / norm
        az = az / norm

        # 估计方向的重力
        vx = 2 * (q1 * q3 - q0 * q2)
        vy = 2 * (q0 * q1 + q2 * q3)
        vz = q0 * q0 - q1 * q1 - q2 * q2 + q3 * q3

        # 错误的领域和方向传感器测量参考方向之间的交叉乘积的总和
        ex = (ay * vz - az * vy)
        ey = (az * vx - ax * vz)
        ez = (ax * vy - ay * vx)

        # 积分误差比例积分增益
        exInt += ex * Ki
        eyInt += ey * Ki
        ezInt += ez * Ki

        # 调整后的陀螺仪测量
        gx += Kp * ex + exInt
        gy += Kp * ey + eyInt
        gz += Kp * ez + ezInt

        # 整合四元数
        q0 += (-q1 * gx - q2 * gy - q3 * gz) * halft
        q1 += (q0 * gx + q2 * gz - q3 * gy) * halft
        q2 += (q0 * gy - q1 * gz + q3 * gx) * halft
        q3 += (q0 * gz + q1 * gy - q2 * gx) * halft

        # 正常化四元数
        norm = math.sqrt(q0 * q0 + q1 * q1 + q2 * q2 + q3 * q3)
        q0 /= norm
        q1 /= norm
        q2 /= norm
        q3 /= norm

        # 获取欧拉角 pitch、roll、yaw
        pitch = math.asin(-2 * q1 * q3 + 2 * q0 * q2) * 57.3
        roll = math.atan2(2 * q2 * q3 + 2 * q0 * q1, -2 * q1 * q1 - 2 * q2 * q2 + 1) * 57.3
        yaw = math.atan2(2 * (q1 * q2 + q0 * q3), q0 * q0 + q1 * q1 - q2 * q2 - q3 * q3) * 57.3

        # 打印姿态角信息以及把姿态角数据写到txt文本中

    print("pry:%.3f,%.3f,%.3f" % (pitch, roll, yaw))
    # aaxx=KalmanFilter(aaxx)
    # aayy=KalmanFilter(aayy)
    # aazz=KalmanFilter(aazz)

    # print(cal_integral(at,aaxall))
    lt,position[0],Vv[0]=cal_tiem(sum(aaxx)/len(aaxx), position[0], lt, Vv[0])
    lt,position[1],Vv[1]=cal_tiem(sum(aayy)/len(aayy), position[1], lt, Vv[1])
    lt,position[2],Vv[2]=cal_tiem(sum(aazz)/len(aazz), position[2], lt, Vv[2])

    str = struct.pack("ffffff", pitch, roll,yaw,position[0]*100,position[1]*100,position[2]*100)
    tctimeClient.send(str)

服务器

import struct
from math import cos, sin
import numpy as np
import matplotlib.pyplot as plt
from socket import *

host = '192.168.3.108'
port = 12345
buffsize = 24
ADDR = (host,port)
tctime = socket(AF_INET,SOCK_STREAM)
tctime.bind(ADDR)
tctime.listen(3)
print('Wait for connection ...')
tctimeClient,addr = tctime.accept()
print("Connection from :",addr)



class Quadrotor():
    def __init__(self, x=0, y=0, z=0, roll=0, pitch=0, yaw=0, size=1, show_animation=True):
        self.p1 = np.array([size / 2, 0, 0, 1]).T
        self.p2 = np.array([-size / 2, 0, 0, 1]).T
        self.p3 = np.array([0, size / 2, 0, 1]).T
        self.p4 = np.array([0, -size / 2, 0, 1]).T

        self.x_data = []
        self.y_data = []
        self.z_data = []
        self.show_animation = show_animation

        if self.show_animation:
            plt.ion()
            fig = plt.figure()
            self.ax = fig.add_subplot(111, projection='3d')

        self.update_pose(x, y, z, roll, pitch, yaw)

    def update_pose(self, x, y, z, roll, pitch, yaw):
        self.x = x
        self.y = y
        self.z = z
        self.roll = roll
        self.pitch = pitch
        self.yaw = yaw
        self.x_data.append(x)
        self.y_data.append(y)
        self.z_data.append(z)

        if self.show_animation:
            self.plot()

    def transformation_matrix(self):
        x = self.x
        y = self.y
        z = self.z
        roll = self.roll
        pitch = self.pitch
        yaw = self.yaw
        return np.array(
            [[cos(yaw) * cos(pitch), -sin(yaw) * cos(roll) + cos(yaw) * sin(pitch) * sin(roll), sin(yaw) * sin(roll) + cos(yaw) * sin(pitch) * cos(roll), x],
             [sin(yaw) * cos(pitch), cos(yaw) * cos(roll) + sin(yaw) * sin(pitch) *
              sin(roll), -cos(yaw) * sin(roll) + sin(yaw) * sin(pitch) * cos(roll), y],
             [-sin(pitch), cos(pitch) * sin(roll), cos(pitch) * cos(yaw), z]
             ])

    def plot(self):
        T = self.transformation_matrix()

        p1_t = np.matmul(T, self.p1)
        p2_t = np.matmul(T, self.p2)
        p3_t = np.matmul(T, self.p3)
        p4_t = np.matmul(T, self.p4)

        plt.cla()

        self.ax.plot([p1_t[0], p2_t[0], p3_t[0], p4_t[0]],
                     [p1_t[1], p2_t[1], p3_t[1], p4_t[1]],
                     [p1_t[2], p2_t[2], p3_t[2], p4_t[2]], 'k.')

        self.ax.plot([p1_t[0], p2_t[0]], [p1_t[1], p2_t[1]],
                     [p1_t[2], p2_t[2]], 'r-')
        self.ax.plot([p3_t[0], p4_t[0]], [p3_t[1], p4_t[1]],
                     [p3_t[2], p4_t[2]], 'r-')

        self.ax.plot(self.x_data, self.y_data, self.z_data, 'b:')

        plt.xlim(-500, 500)
        plt.ylim(-500, 500)
        self.ax.set_zlim(0, 300)

        plt.pause(0.001)
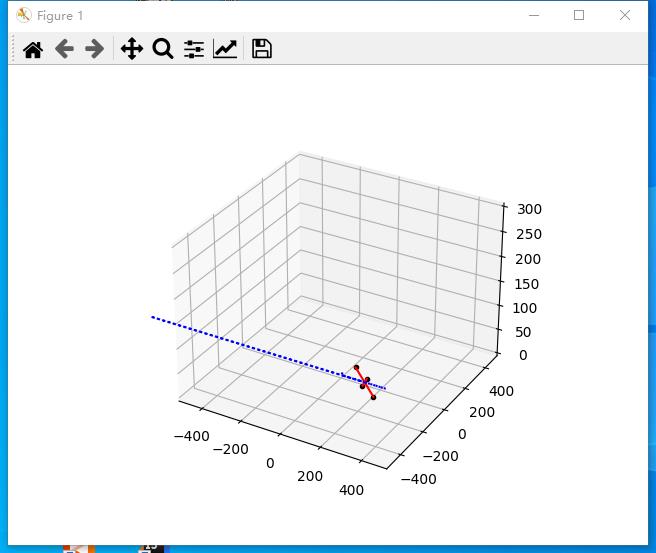
q = Quadrotor(x=5, y=5, z=5, roll=0,pitch=0, yaw=0, size=100, show_animation=True)


for i in range(50000):


    data = struct.unpack('ffffff', tctimeClient.recv(buffsize))
    # print(data)
    # str = struct.pack("fff", pitch, roll,yaw)
    if i%50==0:
        q.update_pose(data[3],data[4],data[5],data[1],data[0],data[2])
        q.plot()
    print(data)
# [{'y': 8.86812294921875, 'x': -3.414131567382812, 'z': 1.6017209106445311}, {'y': 0.8931297709923665, 'x': -1.6870229007633588, 'z': 0.22137404580152673}, 25.941764705882356]

通过二次积分想获取位置信息，但最终x轴一直在增大具体原因不明

结果：


文章作者: 万鲲鹏
文章链接: http://www.mmrsl.cn/2021/12/20/pythonmpu6050/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 万鲲鹏 !
树莓派 python
赏
评论
  目录