机器学习

6 支持向量机

6.1 间隔与支持向量

1. 问题
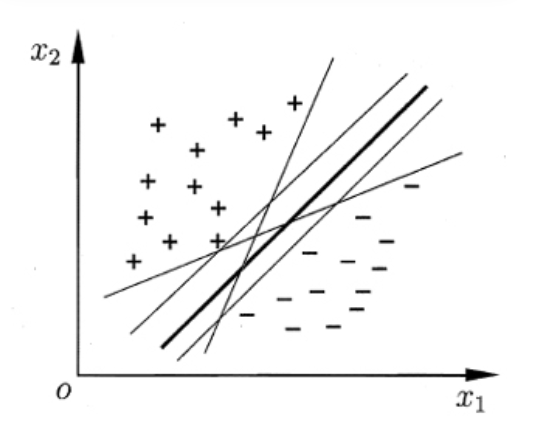
   给定训练样本 $D=\lbrace(x_1,y_1),(x_1,y_1),...,(x_m,y_m)\rbrace,y_i\in \lbrace{-1,+1}\rbrace$分类学习的关键就是基于训练集找出一个划分超平面，将不同类别的样本分开，而这种平面很多，如何选择最好的划分超平面？

图6.1存在划分超平面将两个训练样本分开

正中间那根具有更强的鲁棒性，对未示例的泛化能力更强，因此会获得更好的性能。
划分超平面可以通过如下线性方程来描述：

$$w^Tx+b=0$$

其中$w=(w_1;w_2;...;w_d)$为法向量决定平面的方向，b为位移向项决定平面距离原点的距离。
其中任意一点到超平面的距离可写为

$$r = \frac{|w^Tx+b|}{||w||}$$

1. 支持向量
   距离划分超平面最近的几个训练样本点。且这些点满足以下不等式。
   $ w^Tx_i+b\geq+1, y_i=+1 $
   $w^Tx_i+b\leq-1, y_i=+1$
2. 间隔
   两个异类支持向量到超平面的距离之和： $$r=\frac{2}{||w||}$$
3. 最大间隔
   对应的划分超平面 $$max(r=\frac{2}{||w||}) \\s.t. y_i(w^Tx_i+b)\geq1,i=1,2,...,m$$
4. 最小间隔
   支持向量机基本型 $$min(r=\frac{2}{||w||}) \\s.t. y_i(w^Tx_i+b)\geq1,i=1,2,...,m$$

6.2 对偶问题

6.2.1 对偶问题

突二次规划问题

6.2.2 对偶问题

1. 更有效求解参数w和b的方法:拉格朗日乘子法

• 对svm基本型式子的每个约束添加大于等于零的拉格朗日乘子，得到该问题的拉格朗日函数。
  $ L(w,b,a)=\frac{1}{2}||w||^2+ \sum_{i=1}^ma_i(1-y_i(w^Tx_i+b)) $
  • 令L(w,b,a)对w和b求偏导为零。
    $ w = \sum{i=1}^{m}a_iy_ix_i$
    $ 0=\sum{i=1}^{m}a_iy_i$
  • 将L(w,b,a)中的w和b消去，得到svm基本式子的对偶问题
    ${max}{a}a_i-\frac{1}{2}\sum{i=1}^m\sum{j=1}^ma_ia_jy_iy_jx_i^Tx_j$
    $s.t. \sum{i=1}{m}a_iy_i=0,a_i\geq0,i=1,2,…,m$

1. KKT条件 $$f= \begin{cases} a_i\geq0;\\ y_if(x_i)-1\geq0\\ a_i(y_if(x_i)-1)=0 \end{cases}$$
2. 如何求解对偶问题中的a？
   • 当二次规划问题求解
     算法：二次规划算法
     缺点：问题规模正比例于训练样本数，这样会在实际任务中造成很大开销。
     算法：SMO算法
     选取一对所需更新的变量$a_i和a_j$
     固定$a_j和a_i$ 以外的参数，求解对偶问题获取新的$a_i和a_j$
     不断执行上述两个步骤直到收敛
   1. 如何确定偏移项b？
   • 使用支持向量机求解平均值
     $b=\frac{1}{|s|}\sum{s\in S}(y_s-a_iy_ix_i^Tx_s)$
     $y_s(\sum{i\in S}a_iy_ix_i^Tx_s+b)=1$
     $\lbrace S={i=a_i>0,i=1,2…,m}\rbrace$为所有向量机下标集

     6.2.2 支持向量机的一个重要性质

     训练结束后，大部分训练样本都不需要保留，最终模型与支持向量有关。

     6.3 核函数

     对线性可分问题，可以将原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。

     6.3.1 令y表示x映射后的特征向量

     对偶问题

     6.3.2 支持向量展示

     模型训练最优解可通过训练样本核函数展开。

     6.3.3 常用核函数

   • 线性核函数
   • 多项式核函数
   • 高斯核函数
   • 拉普拉斯核函数
   • sigmoid核函数

     6.3.4 核函数定理

   • 核矩阵总是半正定的
   • 只要一个堆成函数的核函数半正定，就可以被用于核函数
   • 半正定矩阵必然有对应的映射
   • 任何一个核函数都定义了一个希尔伯特空间

     注意：特征空间的好坏对支持向量机至关重要
     “核函数选择”成为支持向量机最大变数

     6.4 软间隔和正则化

     6.4.1 硬间隔

     要求所有样本均满足约束，所有样本必须划分正确。

     6.4.2 软间隔

   1. 解决现实任务：很难确定合适的核函数使得训练到的样本在特征空间中线性可分，或者是否过拟合。
   2. 解决方法：允许部分样本可以出错。允许某些样本不满足约束
      $y_i(w^Tx_i+b)\geq1$
      不满足样本尽可能少。
   3. 新的目标函数

      6.4.3 正则化